Vous vous posez beaucoup de questions sur le logiciel de régression en économétrie par la méthode MCO moindre carré ou ordinaire, Gretel (GNU Regression, Econometrics and Time Series Library – est un logiciel de traitement de données (statistiques et économétrie)

Voici Une synthèse et un exemple complet pour vous

Voici le sujet : » gestion de l’amortissement comptable et le renouvellement des immobilisations »

Première étape

SPECIFICATION DES VARIABLES

Voici les variables prises en compte dans notre étude :
Y : renouvellement de l’outil de production (variable endogène)
X : gestion de l’amortissement comptable (variable exogène)
Y=f(x), comme notre fonction économique

Deuxième étape

ESTIMATION DU MODELE
Nous allons estimer notre modèle par la méthode de moindre carré ordinaire qui consiste à minimiser la somme des carrés résiduels.

Brève explication de la MCO

Méthode de moindre carrée ordinaire (MCO)
Le problème de la régression consiste `à rechercher une relation pouvant éventuellement exister entre les x et les y, par exemple de la forme y = f(x). Lorsque la relation recherchée est affine, c’est-a-dire de la forme yi = ß0+ß1xi, on parle de régression linéaire. Mais même si une telle relation est effectivement présente, les données mesurées ne vérifient pas en général cette relation exactement. Pour tenir compte dans le modèle mathématique des erreurs observées, on considère les données {y1, y2, . . ., yn} comme autant de réalisations d’une variable aléatoire Y et parfois aussi les données {x1, x2, . . . , xn} comme autant de réalisations d’une variable aléatoire X. On dit que la variable Y est la variable d´dépendante ou variable expliquée et que la variable X est la variable explicative.
Les données {(xi, yi), i = 1, . . ., n} peuvent être représentées par un nuage de n points dans le plan (x, y), le diagramme de dispersion. Le centre de gravité de ce nuage peut se calculer facilement : il s’agit du point de coordonnées (x, y) = (n1 Σn i=1xi, n1 Σn i=1yi). Rechercher une relation affine entre les variables X et Y revient à rechercher une droite qui s’ajuste le mieux possible à ce nuage de points. Parmi toutes les droites possibles, on retient celle qui jouit d’une propriété remarquable : c’est celle qui rend minimale la somme des carrés des écarts des valeurs observées yi a la droite yi = axi + b. Si εi représente cet écart, appelé aussi résidu, le principe des moindres carrés ordinaire (MCO) consiste à choisir les valeurs de a et de b qui minimisent.
En réalité cette méthode consiste à minimisé la somme de carré des résidus c’est-à-dire minimiser l’écart entre ce qui a été observé et ce qui devrais être.
Voici concrètement l’estimation a l’aide du logiciel Gretel

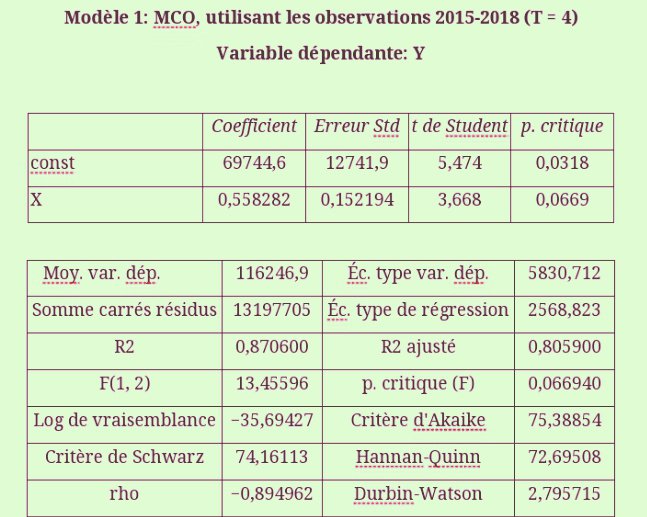
Quelques graphique et l’analyse de de variance (anova)

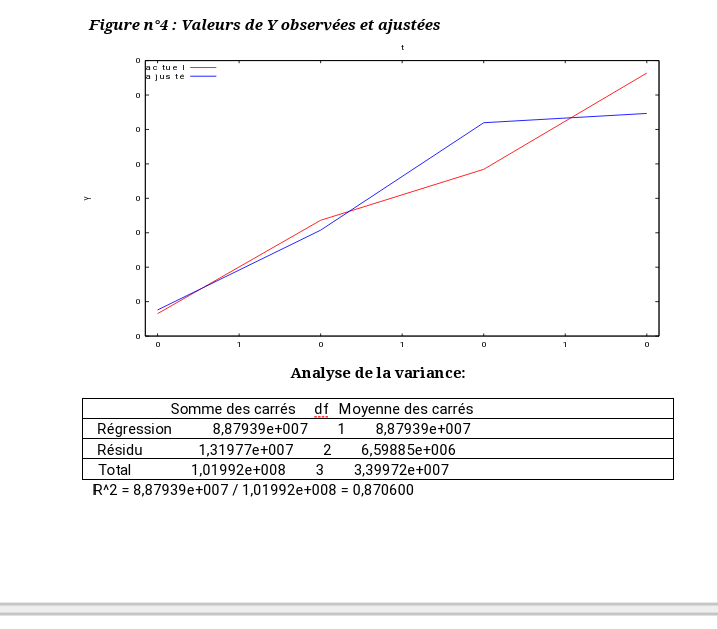
Troisième étape

Interprétation du modèle

Interprétation du model

Vérification de la droite par la moyenne de X
 Qui est la moyenne de Y, d’où il sied de conclure que la droite est bonne
ß0 = : c’est la constante ou l’ordonné à l’origine c’est-à-dire le montant du renouvellement de l’outil de production sans recourir aux amortissements.
ß1 : c’est le taux de croissance ou la variation marginale du renouvellement de l’outil de production lorsqu’il y a une unité de l’amortissement comptable.
Dans la régression simple :
✓ Si ß1est positif alors ß0 est un minimum
✓ Si ß1est négatif alors ß0 est un maximum, cela dit dans notre étude ß0 est un minimum
Cherchons l’erreur :


Le risque de ß0 est de 2568,82
4. Coefficient de détermination R2
Il représente le pourcentage d’explication de la variable exogène X (de l’amortissement comptable)

R^2 = 8,87939e+007 / 1,01992e+008 = 0,870600

Dans notre étude R2 vaux 0,870600 c’est-à-dire, la gestion l’amortissement comptable explique à 87% le renouvellement de l’outil de production.
0,870600
Ceci dit, qu’il existe d’autre variable que nous n’avons pas pu observer et étudier qui explique à  le renouvellement de l’outil de production.

Quatrième étape

Test d’hypothèse avec les tables statistiques

Le test constitue un autre aspect important de notre travail, signalons qu’une hypothèse statistique est un énoncé une affirmation concernant les caractéristiques d’un échantillon.
Un test d’hypothèse autrement appelé test statistique est une démarche qui a pour but de fournir une règle de décision permettant sur base de résultat d’un échantillon de faire un choix entre deux hypothèses :
• H0 : c’est une hypothèse selon laquelle on fixe à priori un paramètre de la population à une valeur particulière. Il est soumis à un test selon lequel il faut établir une règle de décision qui nous conduira à son acceptation ou non.
• H1 : c’est l’alternative ou le contraire de H0

Le seuil de signification du test
La conclusion qui sera déduite des résultats aura un caractère probabiliste, d’où on pourra prendre une décision qu’en ayant conscience qu’il y a certain risque qu’elle soit erronée, ainsi donc ce risque est donné par le seuil de signification. A ce seuil on fait correspondre sur la distribution une région de rejet de H0 appelé aussi région critique, et une autre région appelée région d’acceptation.
Nous proposons dans le cadre de cette analyse le test de Student et de Fisher, du fait que les deux ont donné une même conclusion d’où faute de temps, nous aurions dû le faire en nombre impair (c’est-à-dire 3,5,…) selon les principes économétriques.
a) TEST INDIVIDUEL (Student au seuil de 5%)
H0: ßi = 0 : la gestion de l’amortissement comptable n’a pas d’influence sur le renouvellement de l’outil de production.
H1 : ßi ≠ 0 : la gestion de l’amortissement comptable a de l’influence sur le renouvellement de l’outil de production.
• Voici la condition :
Test unilatéral (droite) si | tcal | >tα, N-K on rejette Ho
tα, N-K : à retrouver dans la table statistique de Student au seuil de 5% il est égal à 3,18
tcal= 5,474
Donc au seuil de 5%, étant donné que la condition | tcal | >tα, N-K est vérifiée nous concluons ce test en rejetant H0 qui stipule que la gestion de l’amortissement comptable n’a pas d’influence sur le renouvellement de l’outil de production, en acceptant H1 qui stipule que la gestion de l’amortissement comptable a de l’influence sur le renouvellement de l’outil de production.
TEST DE FICHER (au seuil de 5%)
Ho :  = 0 : la gestion de l’amortissement comptable n’a pas d’influence sur le renouvellement de l’outil de production.
H1 :  ≠ 0 : la gestion de l’amortissement comptable a de l’influence sur le renouvellement de l’outil de production.
Voici la condition du test :
• Si Fcal > Fth on rejette Ho et on accepte H1
Ficher théorique, trouver sur base des tables statistique dans lesquelles notre degré étant égal à 3 car notre taille de l’échantillon était de 4 =1,3.
Fisher calculé = 
== 13,4
Donc au seuil de 5%, étant donné que la condition Fcal > Fth est vérifiée nous concluons ce test en rejetant H0 qui stipule que la gestion de l’amortissement comptable n’a pas d’influence sur le renouvellement de l’outil de production, en acceptant H1 qui stipule que la gestion de l’amortissement comptable a de l’influence sur le renouvellement de l’outil de production.

Sous réserve d’être contredit par les aînés voici ma contribution!!!!

Nyamayoko ishako Guelord Guelord by les astuces de guelord ishako